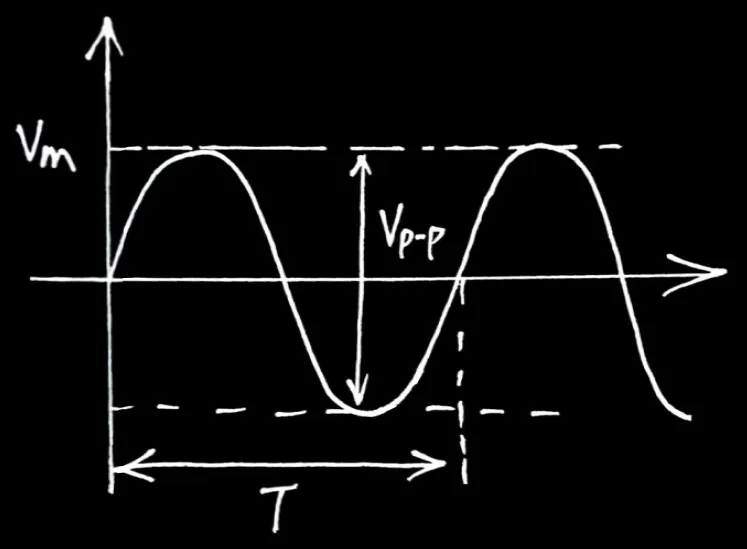
| 有效值Vrms | 平均值Vav | 波峰因數CF | 波形因數FF |
|---|
| 方波 | Vm | Vm | 1 | 1 |
| 正弦波 | 0.707Vm21Vm | 0.636Vmπ2Vm | 1.4142 | 1.1122π |
| 三角波 | 0.577Vm31Vm | 0.5Vm21Vm | 1.7323 | 1.15432 |
CrestFactorCF=VrmsVm
FormFactorFF=VavVrms
🔸 原子
| 導體 | 半導體 | 絕緣體 |
|---|
| 最外層軌道的電子價電子數 | <4 | 4 | >4 |
| 能隙 | 0eV | 1eV | 9eV |
| 電阻溫度係數 | + | − | − |
電子伏特(能量)1eV=1.6×10−19J
軌道上電子數=n:第n層軌道2n2
🔸 半導體
| N 型半導體 | P 型半導體 |
|---|
| 參雜 | 5價 | 3價 |
| 元素 | P磷、As砷、Sb銻 | B硼、Al鋁、Ga鎵、In銦 |
| 別稱 | 給別人電子施體 | 接受別人的電子受體 |
| 離子 | 失去一個電子: 正+ | 接受一個電子: 負− |
| 電性 | 電中性 | 電中性 |
| 多數載子 | 電子 | 電洞 |
本質半導體: ni=n=p
雜質半導體: 本質濃度ni2=電子濃度n×電洞濃度p
載子移動方式
Diffusion擴散: 載子濃度不均引起
Drift飄移: 外加電壓引起
🔸 二極體
材質
| Ge鍺 | Si矽 | GaAs砷化鎵 |
|---|
| 能隙 | 0.66eV | 1.1eV | 1.42eV |
| VD障壁電壓 | 0.2V∼0.3V | 0.6V∼0.7V | 1.1V∼1.2V |
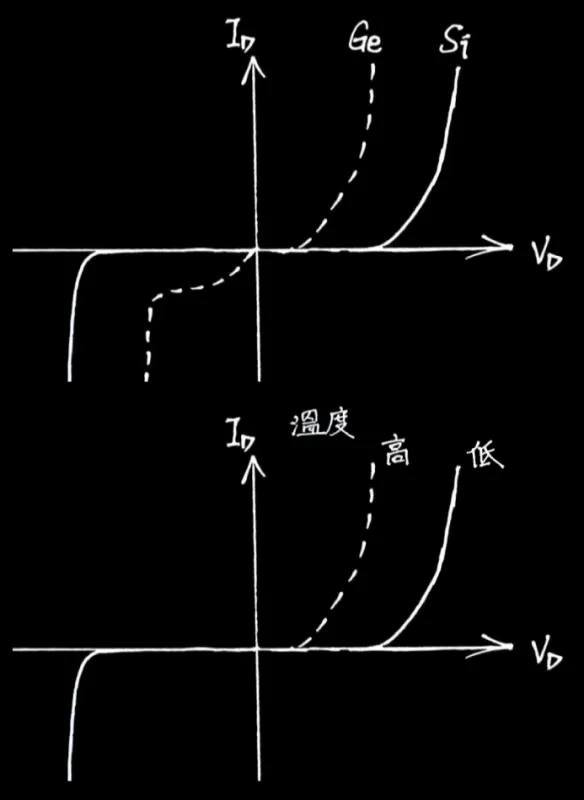
外加偏壓
順向導通電流Id=逆向飽和電流(漏電流)Is×(eηVTVD−1)=當VD>>ηVTIs×eηVTVD
順向偏壓⬆ => 障壁電壓⬇、空乏區寬度⬇
逆向偏壓⬆ => 障壁電壓⬆、空乏區寬度⬆
參雜濃度
參雜濃度⬆ => 障壁電壓⬆、空乏區寬度⬇
溫度效應
| 描述 | 公式 |
|---|
| 切入電壓Von | 溫度上升 1℃,下降 鍺1mV/矽2.5mV | Von2=Von1−or 1mV2.5mV×ΔT |
| 漏電流Is | 溫度上升 10℃,增加 1 倍 | Is2=Is1×210ΔT |
電阻效應
靜態電阻RDCRD=IDVD
動態電阻racrd=IDηVT
K=∘C+273
熱電壓VT=11600K(VT(20∘C)≈25mV)
電容效應
| 偏壓 | 電容 |
|---|
| 順偏 | ID↑⇒擴散電容CD↑ |
| 逆偏 | 逆偏壓↑⇒過度電容CT↓ |
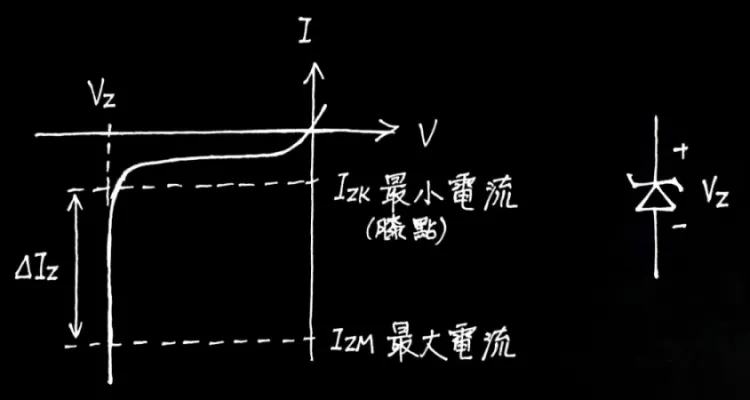
🔸 稽納二極體
| 偏壓 | 稽納二極體 |
|---|
| 順偏 | 視同一般二極體 |
| 逆偏 | 逆偏壓>稽納電壓VZ⇒兩端電壓維持在VZ稽納二極體崩潰 |
| 稽納崩潰 | 累增崩潰 |
|---|
| 崩潰原因 | 穿隧效應 | 撞擊游離 |
| 電壓 | <6V | >6V |
| 溫度係數 | − | + |
🔸 整流電路
| 半波整流 | 中間抽頭 | 橋式整流 |
|---|
| 輸出波形 | 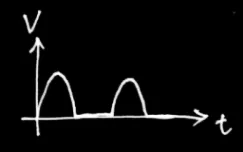 | 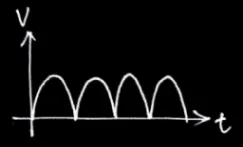 |  |
| 頻率 | f | 2f | 2f |
| PIV | Vm | 2Vm | Vm |
| Vdc | 0.318Vm | 0.636Vm | 0.636Vm |
| Vrms | 0.5Vm | 0.707Vm | 0.707Vm |
| Vr(rms) | 0.385Vm | 0.308Vm | 0.308Vm |
| r% | 121% | 48.4% | 48.4% |
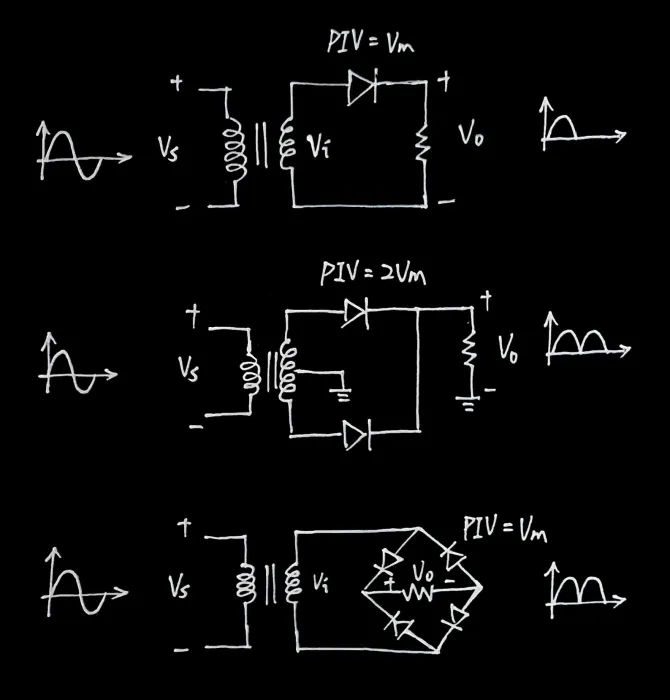
🔸 濾波電路
| 半波整流 | 中間抽頭 | 橋式整流 |
|---|
| PIV | 2Vi(m) | 2Vi(m) | Vi(m) |
| fo | fi | 2fi | 2fi |
| Vr(p−p) | RL×C×foVo(dc) | RL×C×foVo(dc) | RL×C×foVo(dc) |
| Vr(rms) | 23×RL×C×foVo(dc) | 23×RL×C×foVo(dc) | 23×RL×C×foVo(dc) |
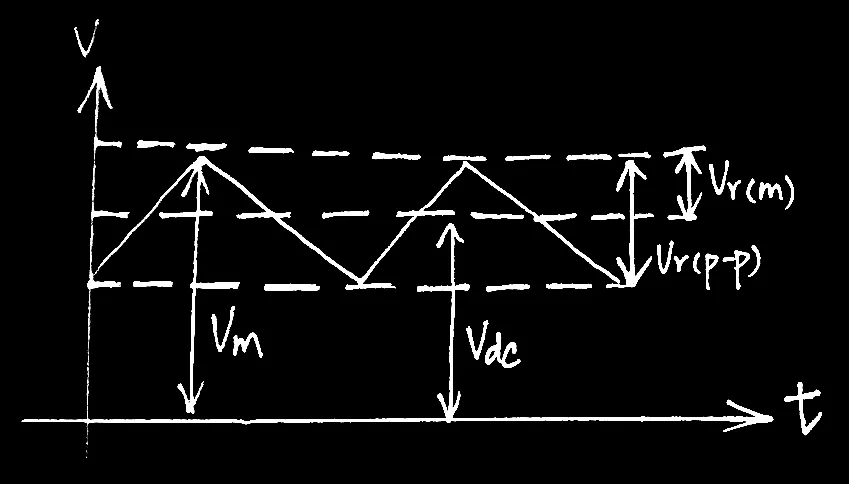
漣波有效值Vr(rms)=Vrms2−Vdc2
漣波因數r%=VdcVr(rms)(越小越好)
Vo(dc)=Vo(m)−Vr(m)
Vr(m)=2Vr(p−p)
🔸 BJT
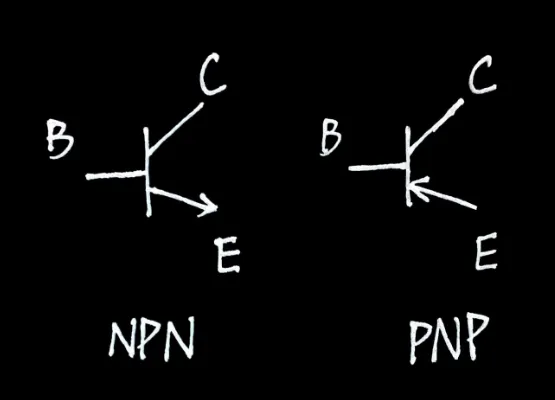
| E | C | B |
|---|
| 描述 | 發射載子 | 收集載子 | 控制載子流 |
| 寬度 | 中 | 大 | 小 |
| 參雜濃度 | 高 | 低 | 中 |
命名
🔹 美系
接面數 N XXXX
ex.
- 1N4007: 二極體
- 2N3569: 電晶體 (NPN)
🔹 日系
| 格式 | 描述 |
|---|
| 1 | 數字 | 0:光二極體(電晶體)、1:二極體
2:電晶體、3:四極體 |
| 2 | 字母 | S:半導體(Semiconductor) |
| 3 | 字母 | A:高頻PNP、B:低頻PNP
C:高頻NPN、D:低頻NPN
F:SCR、G:PUT
J:PMOS、K:NMOS
H:UJT、M:TRIAC |
| 4 | 數字 | 廠商登記序號 |
| 5 | 字母 | 改良品問世順序 |
🔹 其他
工作模式
| 模式 | BE&CB 接面偏壓 | 功能 | 電流/電壓 |
|---|
| 順向主動區 | 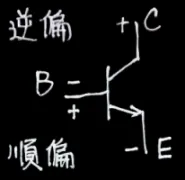 | 放大器 | IC=βIB |
| 逆向主動區 | 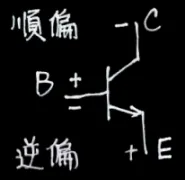 | 邏輯交換電路 | |
| 飽和區 | 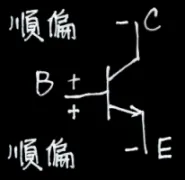 | 開關-ON | IC≤βIB,VCE=0.2V |
| 截止區 | 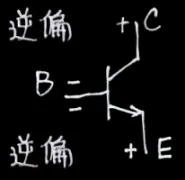 | 開關-OFF | IC=IB=0 |
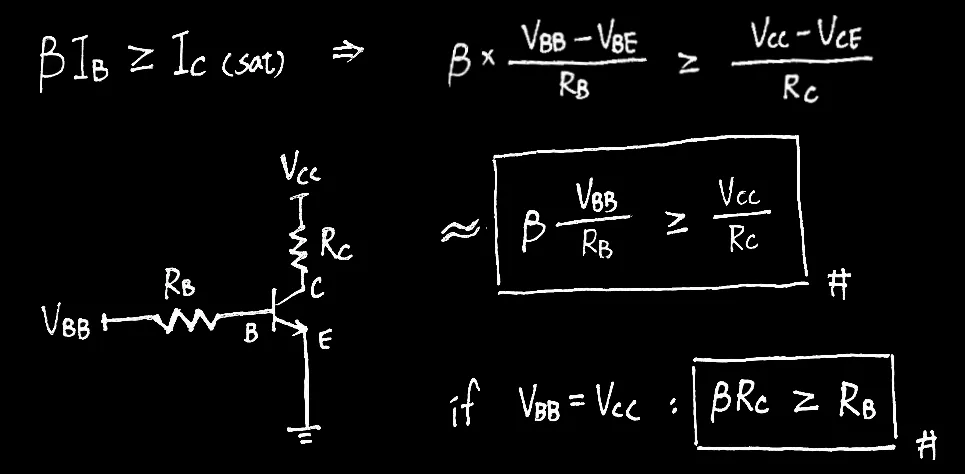
BJT 飽和條件
🔹 βIB≥IC(sat)
🔹 βRC≥RB(ifVCC=VBB)
🔸 BJT 放大器
組態腳位
| 組態 | 共接腳 | 輸入腳 | 輸出腳 | 電流增益 IiIo |
|---|
| CE | E | B | C | β |
| CC | C | B | E | γ |
| CB | B | E | C | α |
🔹 C 極不當輸入端、B 極不當輸出端
組態比較
| CE | CC | CB |
|---|
| 別稱 | | Vo≈Vi電壓緩衝器 | Io≈Ii電流緩衝器 |
| | | |
| Ri | 中 | 大 | 小 |
| Ro | 中 | 小 | 大 |
| | | |
| Av | Av>1中 | Av≈1小 | Av>1大 |
| Ai | Ai>1中 | Ai>1大 | Ai≈1小 |
| Ap | Av>1,Ai>1大 | 小 | 中 |
| | | |
| 頻寬 | 小 | 中 | 大 |
| 相位 | 反 | 同 | 同 |
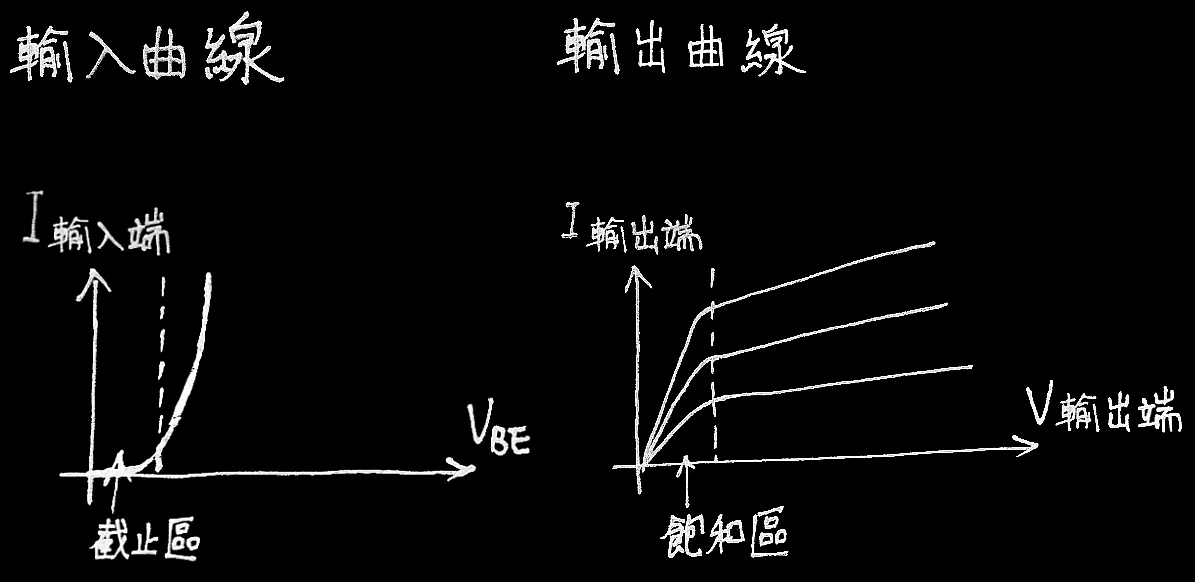
輸入曲線 / 輸出曲線
Ri,Ro
| 放大器 | Ri | Ro |
|---|
| 電壓放大器 | Ri>>Rs,Ri上的分壓越大越大越好 | Ro<<RL,RL上的分壓越大越小越好 |
| 電流放大器 | Ri<<Rs,Ri上的分流越大越小越好 | Ro>>RL,RL上的分流越大越大越好 |
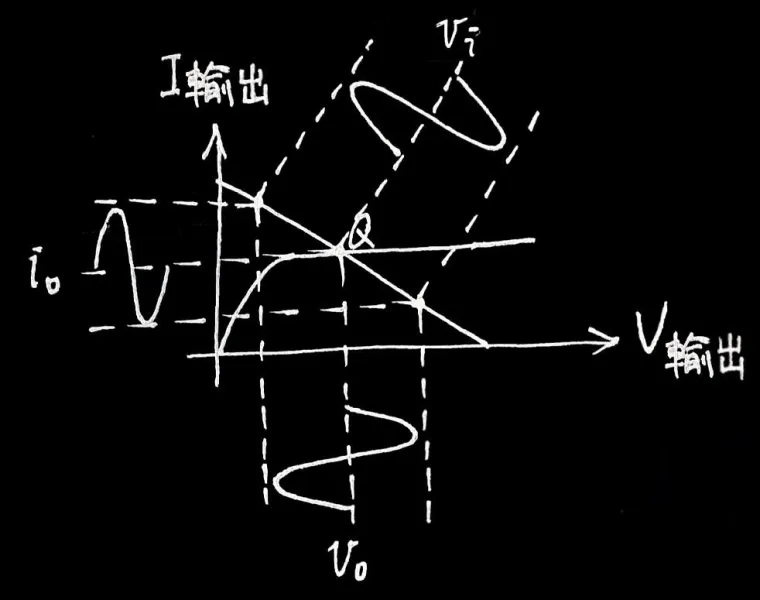
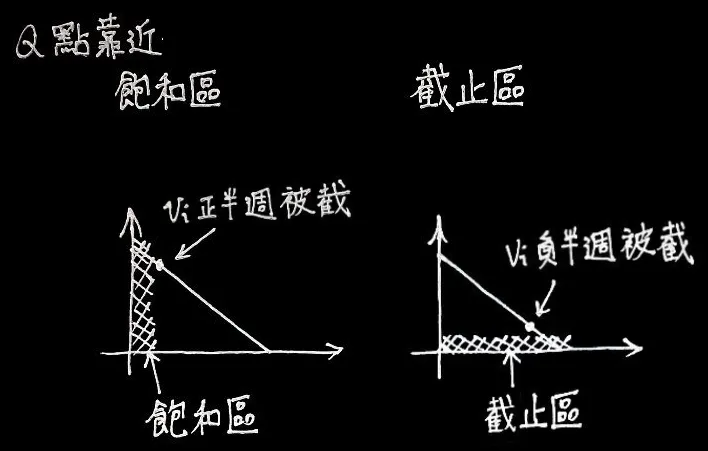
工作點
α,β
| 增益 | 公式 | 範圍 |
|---|
| α | α=IEIC=1+ββ | α≤1 |
| β | β=IBIC=1−αα | |
| γ | γ=β+1 | |
IE=IC+IB
增益
| 增益 | 公式 |
|---|
| 電壓增益 | Av=ViVo |
| 電流增益 | Ai=IiIo=Av×RoRi |
| 功率增益 | Ap=Av×Ai |
Av=BJT輸入端看進去的等效電阻輸出對輸入電流比α,β,γ×輸出端看出去的等效電阻
米勒定理
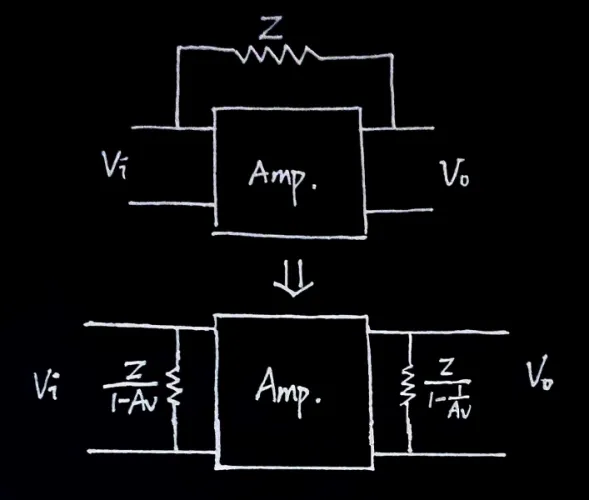
🔸 BJT 串極放大
AvT=Av1×Av2×...×AvnAiT=Ai1×Ai2×...×AinApT=Ap1×Ap2×...×Apn
分貝增益 (dB)
Av(dB)=20logAvAi(dB)=20logAiAp(dB)=10logAp
AvT(dB)=Av1(dB)+Av2(dB)+...+AvnAiT(dB)=Ai1(dB)+Ai2(dB)+...+AinApT(dB)=Ap1(dB)+Ap2(dB)+...+Apn
BJT 串接電路
| 直接耦合 | 疊接 | 達靈頓 |
|---|
| 圖 | | | |
| 功能 | | 提高 CB 組態的 Ri
高頻放大 | 高 Ri
低 Ro
高 Ai |
| Av | Av1×Av1 | Av1×Av1 | ≈1 |
| Ai | Ai1×Ai1 | Ai1×Ai1 | (β1+1)(β2+1) |
🔸 BJT 頻率響應
頻率響應不佳
頻寬
相同放大器串接成 n 級時
fL=2n1−1fL
fH=fH2n1−1
(2n1−1<1)
| 變化 |
|---|
| fL | 變大 |
| fH | 變小 |
| 頻寬 | 縮短 |
🔸 MOSFET
BJT / MOSFET
| BJT | MOSFET |
|---|
| 圖 | | |
| 載子 | 多數載子 + 少數載子雙載子 | 多數載子單載子 |
| 溫度效應 穩定度 | 差 | 佳 |
| 體積 | 大 | 小 |
| 控制方式 | 電流 | 電壓 |
E-MOS / D-MOS
| 增強型E−MOSFET | 空乏型D−MOSFET |
|---|
| 圖 | | |
| 預置通道 | ✖ | ✔ |
| IG | 0 | 0 |
| ID | k×(VGS−VGSt)2 | IDSS×(1−VGSpVGS)2k×(VGS−VGSp)2 |
| k | ∝通道長度L通道寬度W | VGSp2IDSS |
工作區
| 歐姆區 | 截止區 | 飽和區 |
|---|
| 功能 | 電阻、開關ON | 開關OFF | 放大器 |