b592. The Tower of Hanoi

給一正整數 n，代表 河內塔 圓盤的數量
再給兩個數組 A, B，代表 河內塔 圓盤狀態
其中對於 $A_{i},\;B_{i}$
$i$ 代表圓盤的大小（i 越大，圓盤需放在越下面）
$A_{i},\;B_{i} = 1,\;2\;or\;3$ 代表圓盤所在的柱子
求 A 狀態 至 B 狀態 的最少步驟數

---

解法一

🔹 A 狀態 至 B 狀態 的河內塔

化簡

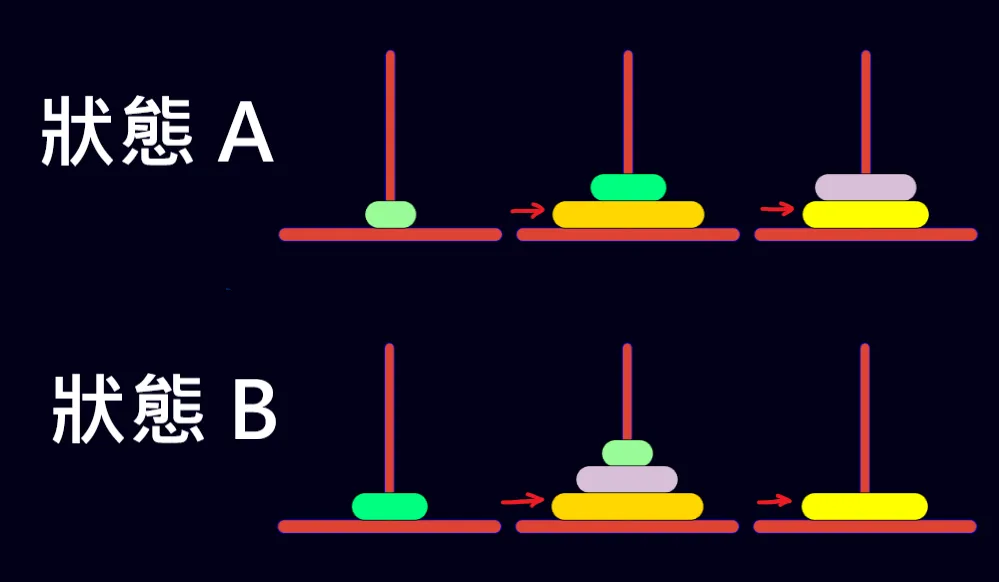
如下圖，可以發現
最大的圓盤 跟 第二大的圓盤 從始至終都沒動過
其他圓盤都比它們小（不會影響到其他圓盤移動）
因此可以直接忽略

考慮 全部在同一柱移至另外一柱 的步驟數

假設有 n 個圓盤，全部在 第 a 柱
現在要把 n 個圓盤全部移至 第 b 柱

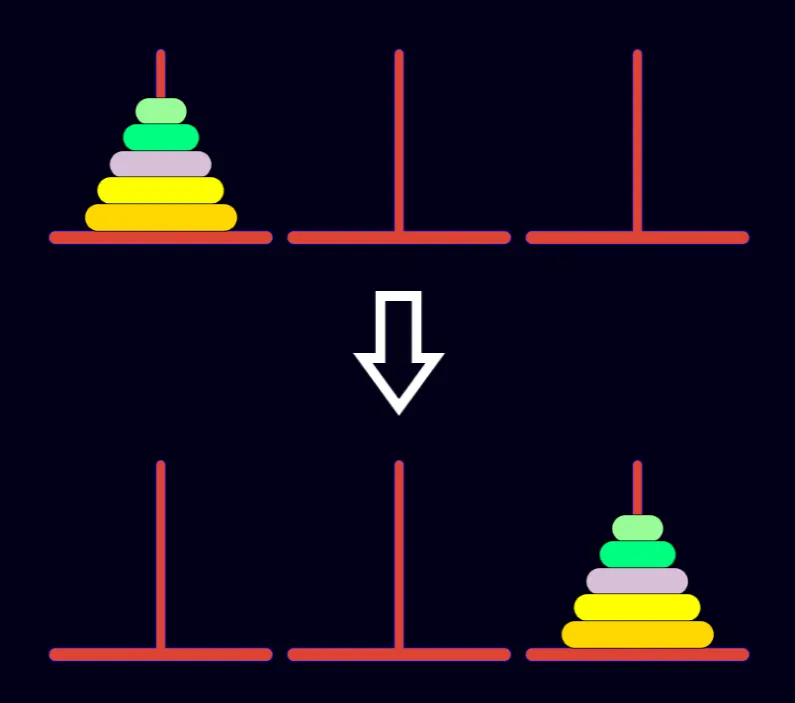
最少步驟數為 $2^{n} - 1$ 步

考慮 全部都在一柱移至任意狀太 的步驟數

假設有 n 個圓盤，全部在 第 k 柱
現在要把 n 個圓盤 移至 A 狀態

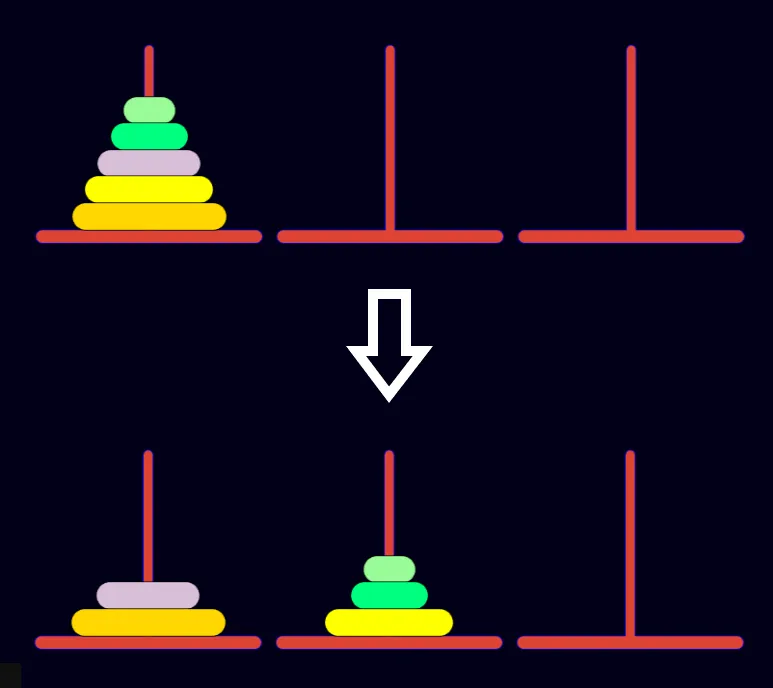
計算最少步驟數的方法如下

判斷 A 狀態 最大圓盤 n 在不在 第 k 柱

如果在：
用化簡原則直接忽略

如果不在：
移動 n 上面的所有圓盤至另一柱（步驟數 $= 2^{n-1} - 1$）
再把 n 移到目標位置（步驟數 $= 1$）
步驟數總和 $= 2^{n-1}$
(記得從新計算 k)

按此規則遍歷所有的圓盤

起始與最終狀態調換，最少步驟數不變

A 狀態 至 B 狀態 的最少步驟數
等於 B 狀態 至 A 狀態 的最少步驟數

🔹 拆解步驟

要讓 A 狀態 變成 B 狀態
我們的步驟可以拆解成

Step 1. 化簡
Step 2. 先把 最大的圓盤以外的圓盤 移至同一柱
Step 3. 移動 最大的圓盤
Step 4. 把同一柱 移至最終狀態

又根據 起始與最終狀態可調換 的性質
Step 2. 可以反過來做
也就是又變成了 全部在同一柱 移至 任意狀太 的步驟數

— — —

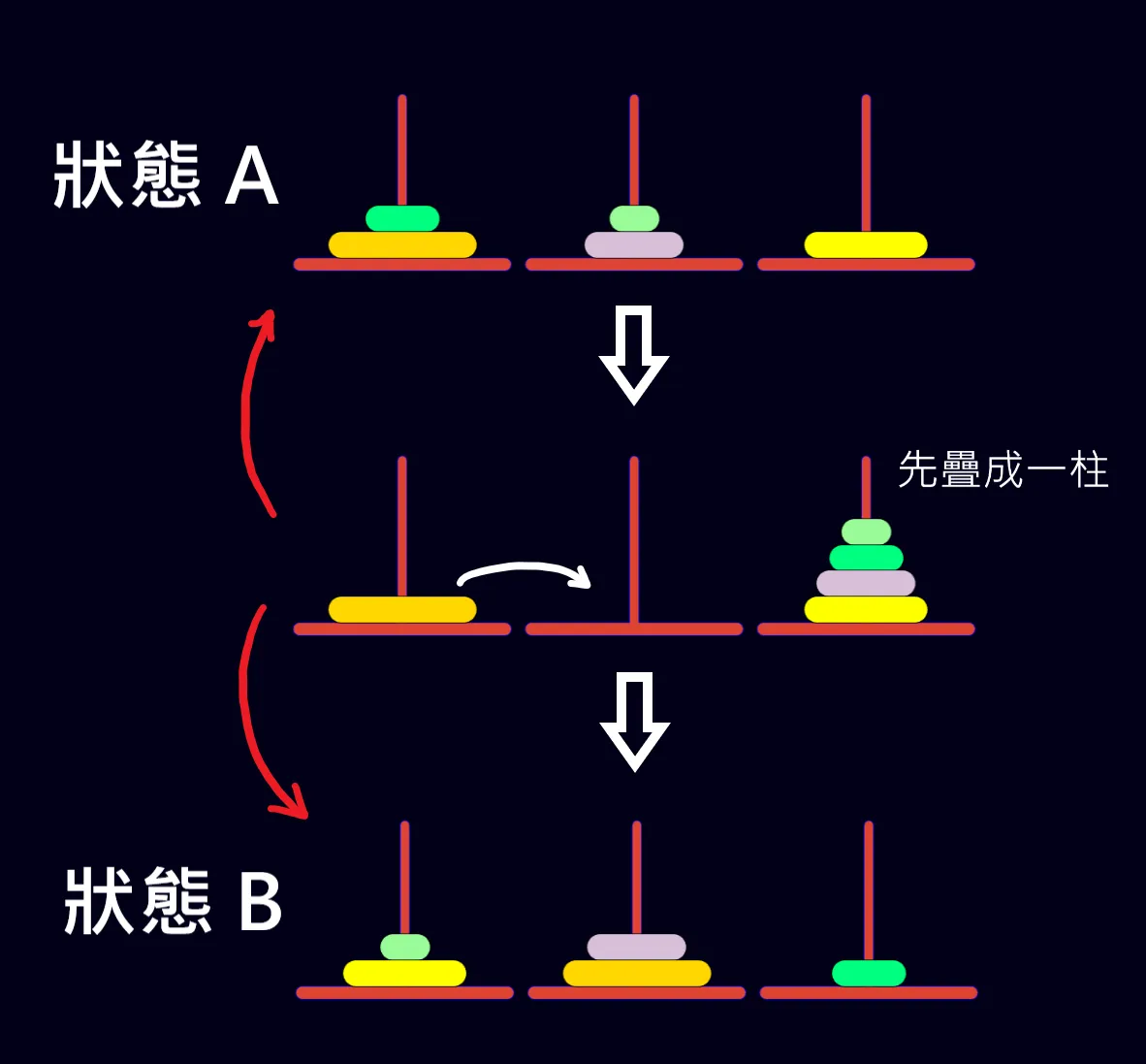
因此答案 = Step 2. + Step 3. + Step 4. 步驟數
Step 3. 為移動大圓盤，步驟數 = 1
Step 2.、Step 4. 實作 cntStep() 函數計算

🔹 Code 解釋

cntStep(vector& a, int k, int idx)
用於計算 全部在第 k 柱 至 A 狀態 的最小步驟數
vector& a 代表一個任意狀態
int k 代表全部圓盤在第 k 柱
int idx 代表只考慮 大小 < idx 的圓盤，（大於的被化簡掉了）

用右移 1 << i 來算 $2^{i}$
另外需要注意 i = 0 ~ n-1
所以計算 $2^{n-1}$ 直接用 i 即可，不能再 -1

✅ 完整代碼

評分結果(參考) ： AC (1ms, 324KB)

#include<bits/stdc++.h>
#define int long long
using namespace std;

int cntStep(vector<int>& a, int k, int idx) {
    if(idx < 0) return 0;

    int step = 0;
    for(int i=idx; i>=0; i--){
        if(a[i] != k){
            step += (1LL << i);
            k = 6-a[i]-k;
        }
    }
    return step;
}

signed main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    int n;
    while(true){
        cin >> n;
        if(n == 0) break;
        
        vector<int> a(n), b(n);
        for(int& i : a) cin >> i;
        for(int& i : b) cin >> i;
        
        int idx = n-1;
        while(idx>=0 && a[idx]==b[idx]){
            idx--;
        }
        int k = 6 - a[idx] - b[idx];
        
        cout << cntStep(a, k, idx-1) + 
                cntStep(b, k, idx-1) + 
                (idx>0 ? 1 : 0) << "\n";
    }
    
    return 0;
}

參考圖使用 https://www.mathsisfun.com/games/towerofhanoi.html 製作